POKOK MATERI TUTORIAL ILMU MATEMATIKA YANG DISESUAIKAN DENGAN STANDAR KOMPETENSI DEPDIKNAS | ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
| P R O B L E M A | ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
MATERI TUTORIAL ILMU MATEMATIKA
Menggunakan kalkulus untuk masalah sehari-hari
Masalah masalah praktis
Yang dimaksud dengan masalah praktis adalah masalah yang mungkin timbul dalam kehidupan sehari-hari. Masalah-masalah yang demikian jarang mempunyai titik-titik singular, untuk masalah-masalah ini nilai maksimum dan minimum biasanya terjadi pada titik stasioner, walaupun titik-titik ujung harus diperiksa.
Berikut adalah dua contoh penggunann kalkulus dalam masalah sehari-hari.

x tidak dapat lebih kecil dari 0 ataupun lebih besar dari 4,5. sehingga masalahnya adalah memaksimumkan V pada [0 ; 4,5]. Titik stasioner ditemukan dengan menetapkan dan menyelesaikan persamaan yang dihasilkan.
dan menyelesaikan persamaan yang dihasilkan.


memperoleh X = 2 atau X = 9, tetapi 9 tidak pada selang [0 ; 4,5] jadi titik kritis hanya terdapat di tiga titik yaitu 0 , 2 , dan 4,5.
pada ujung interval 0 dan 4,5 diperoleh V = 0, pada 2 diperoleh V = 200 sedemikian sehingga kotak mempunyai Volume maksimum 200 incikubik jika X = 2 yaitu apabila kotak berukuran panjang 20 inci, lebar 5 inci , dan tinggi 2 inci.
Misalkan C adalah biaya total dalam rupiah untuk menjalankan truk sejauh k Km.
C = biaya pengemudi + biaya operasi kendaraan


maka :

dengan mengambil
mendapatkan
 artinya pada kecepatan 53 Km per jam adalah total pengeluaran biaya optimum. Tetapi untuk lebih meyakinkan , maka perlu meninjau total biaya (C) pada ketiga titiknya yaitu di v = 40, v = 53, dan v = 60. Caranya silakan substitusi satu persatu harga v ke persamaan
artinya pada kecepatan 53 Km per jam adalah total pengeluaran biaya optimum. Tetapi untuk lebih meyakinkan , maka perlu meninjau total biaya (C) pada ketiga titiknya yaitu di v = 40, v = 53, dan v = 60. Caranya silakan substitusi satu persatu harga v ke persamaan 
Yang dimaksud dengan masalah praktis adalah masalah yang mungkin timbul dalam kehidupan sehari-hari. Masalah-masalah yang demikian jarang mempunyai titik-titik singular, untuk masalah-masalah ini nilai maksimum dan minimum biasanya terjadi pada titik stasioner, walaupun titik-titik ujung harus diperiksa.
Berikut adalah dua contoh penggunann kalkulus dalam masalah sehari-hari.
1. Kotak persegi panjang dibuat dari selembar papan, panjangnya 24 inci dan lebarnya 9 inci, dengan memotong bujur sangkar identik pada keempat pojok dan melipat ke atas sisi-sisinya. Carilah ukuran kotak yang volumenya maksimum. Berapa volume kotak ?Pembahasan 1 : Andai x adalah sisi bujur sangkar yang harus dipotong dan v adalah volume kotak yang dihasilkan, maka :
x tidak dapat lebih kecil dari 0 ataupun lebih besar dari 4,5. sehingga masalahnya adalah memaksimumkan V pada [0 ; 4,5]. Titik stasioner ditemukan dengan menetapkan
memperoleh X = 2 atau X = 9, tetapi 9 tidak pada selang [0 ; 4,5] jadi titik kritis hanya terdapat di tiga titik yaitu 0 , 2 , dan 4,5.
pada ujung interval 0 dan 4,5 diperoleh V = 0, pada 2 diperoleh V = 200 sedemikian sehingga kotak mempunyai Volume maksimum 200 incikubik jika X = 2 yaitu apabila kotak berukuran panjang 20 inci, lebar 5 inci , dan tinggi 2 inci.
2. Menggambarkan suatu masalah yang dialami oleh sebuah perusahaan yang menyalurkan produknya menggunakan kendaraan (misal truk). Dengan bertambahnya kecepatan maka biaya operasional (untuk bahan bakar, pelumas dan lainnya) menjadi bertambah.Pembahasan 2 :
Biaya operasional sebuah kendaraan angkutan diperkirakan sekitarrupiah per kilometer saat dikemudikan dengan kecepatan V Km per jam. Pengemudinya dibayar 1400 rupiah per jam. Pada kecepatan berapakah biaya pengiriman ke suatu kota yang jauhnya k Km akan paling murah ? dengan anggapan bahwa aturan kecepatan yang diperbolehkan
.
Misalkan C adalah biaya total dalam rupiah untuk menjalankan truk sejauh k Km.
C = biaya pengemudi + biaya operasi kendaraan
maka :
dengan mengambil
mendapatkan
PENGGUNAAN ISTILAH DALAM RUMUS VOLUME PRISMA YANG DAPAT MEMBINGUNGKAN SISWA
Fenomena siswa tidak memahami materi matematika dengan baik bukan hanya disebabkan sulitnya materi matematika. Terkadang ketidakpahaman itu juga terjadi juga karena istilah-istilah yang digunakan menyimpang dari kehidupan sehari-hari.
Istilah yang menyimpang dari kehidupan sehari-hari misalnya dalam materi Volume Prisma. Dalam buku-buku pelajaran matematika, biasanya dituliskan rumus volume prisma seperti berikut ini:
Volume Prisma = Luas alas x tinggi
Jadi, penggunaan rumus volume prisma untuk menghitung volume prisma segitiga di bawah ini adalah sebagai berikut.
Volume = Luas alas x tinggi = Luas segitiga ABC x AD
Penggunaan rumus untuk perhitungan di atas tidak bermasalah bagi siswa karena sesuai dengan kehidupan sehari-hari. Segitiga ABC merupakan alas prisma dan AD merupakan tingginya.
Permasalahan akan terjadi jika bangunnya direbahkan.Untuk menghitung volume prisma di atas, maka yang dijadikan sebagai alas adalah segitiga ABC atau segitiga DEF. Wuih, anehkan! Entah sejak kapan istilah alas digunakan untuk menyatakan sesuatu yang tidak terletak di dasar bangun.
Lebih-lebih lagi untuk tinggi prisma. Untuk menghitung volume prisma, maka yang merupakan tingginya adalah AD atau BE, atau CF. Aneh lagi kan! tinggi ko mendatar.
Kalau kita lihat pada bangun prisma di atas, seharusnya yang dikatakan alas adalah segiempat ACFD. Begitu pula tinggi, seharusnya yang memenuhi adalah AB. Membingungkan bukan! Wajar saja kalau siswa keliru menghitung volume bangun prisma.
Inilah yang saya maksud adanya penyimpangan istilah-istilah matematika dengan kehidupan sehari-hari. Kalau ini dibiarkan maka lama-kelamaan akan membuat siswa merasa matematika tidak sesuai dengan kehidupan sehari-hari. Tentunya ini tidak kita inginkan bukan...........
TIDAK PERNAH ADA OPERASI 0/0 DALAM LIMIT
Kita mengetahui bahwa 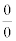 memberikan hasil yang tidak terdefinisi. Tapi jika kita menyelesaikan persoalan limit, sepertinya kita melakukan operasi
memberikan hasil yang tidak terdefinisi. Tapi jika kita menyelesaikan persoalan limit, sepertinya kita melakukan operasi 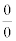 . Contohnya dalam kasus berikut:
. Contohnya dalam kasus berikut:
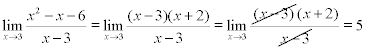 Pada kasus di atas, untuk x -> 3, kita diperkenankan mencoret (x – 3) yang sepertinya memberi kesan diperbolehkannya
Pada kasus di atas, untuk x -> 3, kita diperkenankan mencoret (x – 3) yang sepertinya memberi kesan diperbolehkannya 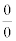 . Benarkah demikian?
. Benarkah demikian?
***
Melalui cerita di bawah ini mudah-mudahan kita dapat memahami alasannya.
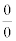 memberikan hasil yang tidak terdefinisi. Tapi jika kita menyelesaikan persoalan limit, sepertinya kita melakukan operasi
memberikan hasil yang tidak terdefinisi. Tapi jika kita menyelesaikan persoalan limit, sepertinya kita melakukan operasi 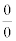 . Contohnya dalam kasus berikut:
. Contohnya dalam kasus berikut: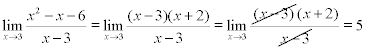
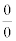 . Benarkah demikian?
. Benarkah demikian?***
Melalui cerita di bawah ini mudah-mudahan kita dapat memahami alasannya.
Anak-anak yang hidup di perkotaan biasanya sulit menemukan tanah lapang tempat bermain layangan. Oleh karena itu mereka biasanya menjadikan atap rumah sebagai tempat bermain layangan.
Pada saat saya dan teman-temanku sering bermain layangan di atas sebuah rumah kosong. Rumah kosong tersebut sudah tua dan banyak kerusakan karena lama ditinggalkan dan tidak dirawat oleh pemiliknya. Kerusakan itu tidak hanya pada bagian dalam tetapi juga pada atapnya. Ada sebuah lubang yang cukup besar dan jika tidak berhati-hati maka kami akan jatuh terperosok ke dalam. Maklum, besarnya diameter lubang melebihi dua kali besarnya diameter tubuh kami.
Suatu hari pamanku ikut bermain di atap rumah kosong tersebut. Saat asyik bermain, tiba-tiba pamanku memberikan sebuah sayembara. Hadiahnya juga tidak tanggung-tanggung dan cukup wah bagi kami yang saat itu ada tiga orang. Mau tahu? Sebuah coklat silverqueen yang gede.
Suatu hari pamanku ikut bermain di atap rumah kosong tersebut. Saat asyik bermain, tiba-tiba pamanku memberikan sebuah sayembara. Hadiahnya juga tidak tanggung-tanggung dan cukup wah bagi kami yang saat itu ada tiga orang. Mau tahu? Sebuah coklat silverqueen yang gede.
”Kalian mau coklat ini?” pamanku berbicara sambil menunjukkan sebuah coklat silverqueen yang gede dan masih terbungkus rapi dalam kemasannya.
Sambil meneguk liur tanda ngiler kami serempak menjawab, ”mau”.
”Tapi ada syaratnya” terang paman sambil menyembunyikan coklatnya.
”Apa syaratnya?” tanyaku sambil mengerenyitkan dahi.
Pamanku tak segera menjawab dan hanya tersenyum.
”Apa syaratnya pama....n?” salah satu temanku ikut mendesak paman. Terang saja kami terus mendesak karena takut kalau pamanku menarik keputusannya.
”Begini. Kalian lihat lubang besar itu” jawab paman sambil melemparkan pandangan ke lubang dan menunjuknya dengan bibir.
”mmmh. Ko mulut dijadikan penunjuk sih, bukannya jari telunjuk. Seperti ikan lohan jadinya” kataku dalam hati tapi tak berani ketawa. Takut tersinggung. Kedua temanku pun tersenyum tertahan.
Kemudian kami bersama memandang lubang yang dimaksud pamanku.
”Kalau kalian dapat tepat berdiri di atas lubang itu dan tidak terjatuh ke dalamnya maka coklat ini akan aku berikan” lanjut pamanku.
”Kalau kalian dapat tepat berdiri di atas lubang itu dan tidak terjatuh ke dalamnya maka coklat ini akan aku berikan” lanjut pamanku.
”Begitu. Kami boleh bekerjasama kan?” tanya temanku
”Boleh” jawab pamanku sambil mengangguk.
Kami bertiga bergegas bergerak menuju lubang. Kami bekerjasama berusaha agar berdiri di atas lubang tapi tidak masuk ke dalam. Namun, dari arah manapun kami mendekati lubang tetap saja kami tidak bisa. Ya, yang dapat kami lakukan hanya mendekati lubang sekeras apapun kami bekerja sama. Entah itu saling berpegangan dan sebagainya.
Yah. Seperti peribahasa bagai punguk merindukan bulan, kami pun tidak mendapatkan coklat itu. Hanya mampu berimajinasi saja.
***
Penggalan cerita di atas dapat kita ibaratkan dengan limit. Jika lubang diibaratkan sebagai 3, maka yang dikatakan x mendekati 3 (lambangnya x->3) adalah seperti anak-anak tersebut yang bergerak mendekati lubang. Mereka hanya mampu mendekati lubang tanpa pernah dapat berdiri di atas lubang.
***
Penggalan cerita di atas dapat kita ibaratkan dengan limit. Jika lubang diibaratkan sebagai 3, maka yang dikatakan x mendekati 3 (lambangnya x->3) adalah seperti anak-anak tersebut yang bergerak mendekati lubang. Mereka hanya mampu mendekati lubang tanpa pernah dapat berdiri di atas lubang.
Jadi, yang dimaksud dengan x -> 3 adalah x hanya semakin mendekati 3 baik dari kiri maupun kanan tetapi tidak pernah mencapai 3. Artinya tidak akan pernah x = 3.
Oleh karena itu, jika x -> 3 (x hanya mendekati 3) maka (x – 3) tidak akan pernah sama dengan 0. Ini artinya melakukan operasi 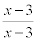 diperbolehkan karena tidak sama dengan
diperbolehkan karena tidak sama dengan 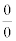 .
.
Nah, sekarang sudah tahu kan alasannya.
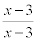 diperbolehkan karena tidak sama dengan
diperbolehkan karena tidak sama dengan 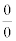 .
.Membuat Media Interaktif untuk Menjelaskan Konsep Sudut dengan Mathematica
Dalam artikel kali ini, kita akan mencoba membuat media interaktif yang dapat digunakan untuk memahami konsep sudut dengan Mathematica. Dengan media ini nanti, siswa diharapkan dapat melihat efek perubahan besar sudut mulai dari 0-360 derajad.
Untuk mempermudah pemahaman dalam proses pembuatannya, penjelasan akan diberikan secara tahap demi tahap.
Sebagai ilustrasi, perhatikan hasil akhir dari media yang akan kita buat di bawah ini.
If you can see this, then you might need a Flash Player upgrade or you need to install Flash Player if it's missing. Get from Adobe.
OK.. kita mulai saja pembuatannya.
Langkah pertama kita harus buat perintah untuk membuat animasi di Mathematica.
Lho… kok masih kosong parameter-parameternya? Sabar teman… kita baru mulai langkah awal.
Karena kita akan membuat animasi perubahan sudut dari 0 – 360 derajad, maka kita anggap animasi ini memiliki 361 frame, Tapi bagaimana menyatakannya dalam Mathematica? Ya… kita tambahkan saja dalam parameter perintah di atas
Apa maksud dari parameter {sudut, 0, 360, 1}? Maksudnya adalah perubahan sudutnya mulai dari 0 – 360 dengan tingkat kenaikan sudutnya 1 derajad.
Trus… obyek apa yang pertama kali dibuat? Mmm… kita bisa membuat obyek garis merah putus-putus, yang horizontal terlebih dahulu. Garis ini digunakan sebagai garis bantu untuk membaca sudut.

Garis tersebut dimisalkan menghubungkan titik (-1, 0) dan (1, 0).
Selanjutnya kita buat juga garis vertikalnya.

Berikutnya, kita buat garis hitam horizontal yang bersifat statis.

Nah… setelah garis sudut statis sudah dibuat, berikutnya garis sudut yang dinamis (yang bergerak). Garis ini kita buat dengan panjang 1 satuan. Bagaimana cara membuatnya? Mmm.. sebentar.. Perintah Mathematica untuk membuat garis adalah Line[]. Garis ini menghubungkan 2 buah titik. Lantas… titik mana saja untuk membuat garis dinamis ini? Salah satu titiknya jelas ada di (0, 0) karena merupakan titik pangkal perputaran. Selanjutnya apa titik yang kedua? Bagaimana pula hubungan titik tersebut dengan sudut? Maksudnya jika sudut yang dibentuk antara garis hitam statis dengan garis dinamis adalah m derajad, bagaimana posisi titik kedua untuk membuat garis dinamis ini? OK.. perhatikan ilustrasi berikut ini

Dari gambar di atas, dapat dituliskan
cos(m) = x/1 = x
sin(m) = y/1 = y
Sehingga titik (x, y) kaitannya dengan sudut yang dibentuk garis dinamis terhadap garis statis adalah (cos(m), sin(m)), dengan m nya adalah sudut. Dengan demikian garis dinamis ini menghubungkan titik (0, 0) dan (cos(m), sin(m)). Namun ingat bahwa nilai sudut m pada Mathematica adalah dalam satuan radian, sedangkan satuan sudut yang kita gunakan adalah derajad. Maka kita harus konversi m ke dalam derajad, yaitu Pi*m/180. Sehingga titik untuk membuat garis dinamis ini adalah (0, 0) dan (cos(Pi*m/180), sin(Pi*m/180)). Nah… kita buat di Mathematicanya. Ingat… kita sesuaikan variabelnya, karena gunakan variabel bernama ‘sudut’, maka m nya kita ganti dengan ‘sudut’, dimana nilai ‘sudut’ ini bergerak dari 0 – 360 derajad.
Apabila perintah di atas kita jalankan, maka animasi sudah bisa dijalankan dengan menggeser slider yang ada. Namun, alangkah cantiknya seandainya kita gambar pula kurva lengkung yang menunjukkan sudut yang dibentuk antara dua garis hitam.
Untuk membuat kurva lengkung ini, kita gunakan perintah Circle[]. Perintah ini pada dasarnya digunakan untuk membuat lingkaran, sesuai namanya. Namun dapat pula kita membuat kurva lengkung menggunakan perintah ini. Sebagai contoh misalkan diberikan perintah Circle[{0, 0}, 1, {0, Pi}]. Perintah ini akan membuat lingkaran dengan pusat (0, 0), panjang jari-jari 1 satuan, dan kurva yang dibentuk mulai dari sudut 0 s/d Pi radian. Dengan demikian perintah ini akan menghasilkan kurva lengkung 1/2 lingkaran.
Nah… sekarang kita kaitkan dengan kasus yang sedang kita kerjakan. Dalam hal ini kurva lengkung yang akan dibuat mestinya berada di pusat (0, 0), panjang jari-jarinya kurang dari 1 satuan (misal kita ambil 0.25 satuan), dan sudut awal kurva lengkung adalah 0 radian (0 derajad). Yang menjadi masalah adalah sampai sudut berapakah kurva lengkung ini dibuat? Ya… tentu saja sampai m radian atau Pi*m/180 derajad. Sehingga perintah untuk membuat kurva lengkung ini adalah Circle[{0, 0}, 0.25, {0, Pi*m/180}]. Sekarang bisa kita tambahkan ke perintah Mathematicanya
OK… jadi deh… selamat bersenang-senang dengan media ini. Anda dapat melihat nilai sudutnya atau bahkan mengganti nilai sudut sesuai yang diinginkan. Bagaimana caranya? Cukup klik tanda + di sebelah kanan slider (scroller untuk menggeser sudut).
Untuk mempermudah pemahaman dalam proses pembuatannya, penjelasan akan diberikan secara tahap demi tahap.
Sebagai ilustrasi, perhatikan hasil akhir dari media yang akan kita buat di bawah ini.
If you can see this, then you might need a Flash Player upgrade or you need to install Flash Player if it's missing. Get from Adobe.
OK.. kita mulai saja pembuatannya.
Langkah pertama kita harus buat perintah untuk membuat animasi di Mathematica.
1.Manipulate[Graphics[], {}]Karena kita akan membuat animasi perubahan sudut dari 0 – 360 derajad, maka kita anggap animasi ini memiliki 361 frame, Tapi bagaimana menyatakannya dalam Mathematica? Ya… kita tambahkan saja dalam parameter perintah di atas
1.Manipulate[Graphics[], {sudut, 0, 360, 1}]Trus… obyek apa yang pertama kali dibuat? Mmm… kita bisa membuat obyek garis merah putus-putus, yang horizontal terlebih dahulu. Garis ini digunakan sebagai garis bantu untuk membaca sudut.
1.Manipulate[Graphics[{{Red, Dashed, Line[{{-1, 0}, {1, 0}}]}}],2.{sudut, 0, 360, 1}]Garis tersebut dimisalkan menghubungkan titik (-1, 0) dan (1, 0).
Selanjutnya kita buat juga garis vertikalnya.
1.Manipulate[Graphics[{{Red, Dashed, Line[{{-1, 0}, {1, 0}}]},2.{Red, Dashed, Line[{{0, 1}, {0, -1}}]}}],3.{sudut, 0, 360, 1}]Berikutnya, kita buat garis hitam horizontal yang bersifat statis.
1.Manipulate[Graphics[{{Red, Dashed, Line[{{-1, 0}, {1, 0}}]},2.{Red, Dashed, Line[{{0, 1}, {0, -1}}]},3.{Line[{{0, 0}, {1, 0}}]}}],4.{sudut, 0, 360, 1}]Nah… setelah garis sudut statis sudah dibuat, berikutnya garis sudut yang dinamis (yang bergerak). Garis ini kita buat dengan panjang 1 satuan. Bagaimana cara membuatnya? Mmm.. sebentar.. Perintah Mathematica untuk membuat garis adalah Line[]. Garis ini menghubungkan 2 buah titik. Lantas… titik mana saja untuk membuat garis dinamis ini? Salah satu titiknya jelas ada di (0, 0) karena merupakan titik pangkal perputaran. Selanjutnya apa titik yang kedua? Bagaimana pula hubungan titik tersebut dengan sudut? Maksudnya jika sudut yang dibentuk antara garis hitam statis dengan garis dinamis adalah m derajad, bagaimana posisi titik kedua untuk membuat garis dinamis ini? OK.. perhatikan ilustrasi berikut ini
Dari gambar di atas, dapat dituliskan
cos(m) = x/1 = x
sin(m) = y/1 = y
Sehingga titik (x, y) kaitannya dengan sudut yang dibentuk garis dinamis terhadap garis statis adalah (cos(m), sin(m)), dengan m nya adalah sudut. Dengan demikian garis dinamis ini menghubungkan titik (0, 0) dan (cos(m), sin(m)). Namun ingat bahwa nilai sudut m pada Mathematica adalah dalam satuan radian, sedangkan satuan sudut yang kita gunakan adalah derajad. Maka kita harus konversi m ke dalam derajad, yaitu Pi*m/180. Sehingga titik untuk membuat garis dinamis ini adalah (0, 0) dan (cos(Pi*m/180), sin(Pi*m/180)). Nah… kita buat di Mathematicanya. Ingat… kita sesuaikan variabelnya, karena gunakan variabel bernama ‘sudut’, maka m nya kita ganti dengan ‘sudut’, dimana nilai ‘sudut’ ini bergerak dari 0 – 360 derajad.
1.Manipulate[Graphics[{{Red, Dashed, Line[{{-1, 0}, {1, 0}}]},2.{Red, Dashed, Line[{{0, 1}, {0, -1}}]},3.{Line[{{0, 0}, {1, 0}}]},4.{Line[{{0, 0}, {Cos[sudut Pi/180], Sin[sudut Pi/180]}}]}}],5.{sudut, 0, 360, 1}]Untuk membuat kurva lengkung ini, kita gunakan perintah Circle[]. Perintah ini pada dasarnya digunakan untuk membuat lingkaran, sesuai namanya. Namun dapat pula kita membuat kurva lengkung menggunakan perintah ini. Sebagai contoh misalkan diberikan perintah Circle[{0, 0}, 1, {0, Pi}]. Perintah ini akan membuat lingkaran dengan pusat (0, 0), panjang jari-jari 1 satuan, dan kurva yang dibentuk mulai dari sudut 0 s/d Pi radian. Dengan demikian perintah ini akan menghasilkan kurva lengkung 1/2 lingkaran.
Nah… sekarang kita kaitkan dengan kasus yang sedang kita kerjakan. Dalam hal ini kurva lengkung yang akan dibuat mestinya berada di pusat (0, 0), panjang jari-jarinya kurang dari 1 satuan (misal kita ambil 0.25 satuan), dan sudut awal kurva lengkung adalah 0 radian (0 derajad). Yang menjadi masalah adalah sampai sudut berapakah kurva lengkung ini dibuat? Ya… tentu saja sampai m radian atau Pi*m/180 derajad. Sehingga perintah untuk membuat kurva lengkung ini adalah Circle[{0, 0}, 0.25, {0, Pi*m/180}]. Sekarang bisa kita tambahkan ke perintah Mathematicanya
1.Manipulate[Graphics[{{Red, Dashed, Line[{{-1, 0}, {1, 0}}]},2.{Red, Dashed, Line[{{0, 1}, {0, -1}}]},3.{Line[{{0, 0}, {1, 0}}]},4.{Line[{{0, 0}, {Cos[sudut Pi/180], Sin[sudut Pi/180]}}]},5.{Dashed, Circle[{0, 0}, 0.25, {0, sudut Pi/180}]}}],6.{sudut, 0, 360, 1}]Trik Belajar matematika
Trik Belajar matematika
Siapa yang ingin cepat bisa menguasai pelajaran Matematika? Berikut ini saya share ilmu tentang bagaimana cara praktis belajar matematika. Mudah-mudahan berguna bagi kalian. Selamat menikmati.
1. Pahami materi (cermati semua informasi yang ada)
2. perlu keberanian (berani mencoba), dengan ini kita akan dapat memahami dan menjadi suatu pengalaman yang sulit terlupakan
ini trik belajar
1. Baca semua yang disampaikan dalam buku
2. pahami teori atau rumus-rumus yang ada
3. kerjakan soal dari yang termudah (biasanya buku sudah mengurutkannya dalam soal)
4. bila mendapat kesulitan, coba periksa dan pahami teori atau rumus-rumusnya kembali
5. kalau langkah 1-4 tidak ada kendala, anda harus siap-siap melihat model-model soal yang lain sebagai pengalaman. Bila konsep dasar sudah dimengerti, tingkat soal-soal matematika hanya bermain pada mode-model soal.
6. 1-4 anda telah menjadai matematika-mania, jika ditambah dengan no 5, anda telah mahir matematika.
Menyelesaikan pertidaksamaan
Langkah biasa
1. Menyederhanakan pertaksamaan
2. Mencari nilai x (menentukan nilai fariabel)
3. dari satu dan dua, sehingga dapat ditentukan batas-batas x yang memenuhi pertaksamaan.
Menyelesaikan soal
1. Gunakan informasi atau data yang ada dalam soal.
2. Hubungkan informasi atau data yang ada dengan teori/rumus yang dapat digunakan dalam menyelesaikan soal-soal tersebut. Ingat!, biasanya soal yang bagus tidak berhubungan langsung dengan
1. Pahami materi (cermati semua informasi yang ada)
2. perlu keberanian (berani mencoba), dengan ini kita akan dapat memahami dan menjadi suatu pengalaman yang sulit terlupakan
ini trik belajar
1. Baca semua yang disampaikan dalam buku
2. pahami teori atau rumus-rumus yang ada
3. kerjakan soal dari yang termudah (biasanya buku sudah mengurutkannya dalam soal)
4. bila mendapat kesulitan, coba periksa dan pahami teori atau rumus-rumusnya kembali
5. kalau langkah 1-4 tidak ada kendala, anda harus siap-siap melihat model-model soal yang lain sebagai pengalaman. Bila konsep dasar sudah dimengerti, tingkat soal-soal matematika hanya bermain pada mode-model soal.
6. 1-4 anda telah menjadai matematika-mania, jika ditambah dengan no 5, anda telah mahir matematika.
Menyelesaikan pertidaksamaan
Langkah biasa
1. Menyederhanakan pertaksamaan
2. Mencari nilai x (menentukan nilai fariabel)
3. dari satu dan dua, sehingga dapat ditentukan batas-batas x yang memenuhi pertaksamaan.
Menyelesaikan soal
1. Gunakan informasi atau data yang ada dalam soal.
2. Hubungkan informasi atau data yang ada dengan teori/rumus yang dapat digunakan dalam menyelesaikan soal-soal tersebut. Ingat!, biasanya soal yang bagus tidak berhubungan langsung dengan
rumus (lansung bisa didapat hasil), tapi ada beberapa tahap untuk sampai ke-penyelesaian akhir.
Cara lain Menyelesaikan soal pilihan ganda pertidaksamaan
1. Pilihlan sebuah bilangan yang menghasilkan perhitungan yang mudah bila bilangan itu disubtitusikan ke dalam pertaksamaan
2. subtitusikan bilangan yang kita pilih itu ke dalam pertaksamaan dan kemudian periksa kebenaran ketaksamaan yang terjadi.
3. bila ketaksamaan yang terjadi itu benar, himpunan penyelesaian yang benar harus mengandung bilangan yang kita pilih tadi. Namun bila salah, kesimpulannya adalah sebaliknya.
Penyelesaian persamaan kuadrat soal pilihan ganda
• pertama-tama kita ganti dulu peubah yang tidak diketahui nilainya dengan sebuah bilangan nyata sembarang. Bentuk yang terjadi kemudian kita analisis dengan menggunakan rumus-rumus dasar.
1. ajukan pertanyaan yang berkaitan dengan data maupun informasi yang tersedia di dalam soal.
2. Mengambil kesimpulan dengan data atau informasi yang ada dalam soal.
3. Menciptakan cara mudah atau mempercepat untuk menyelesaikan
1. simak dengan cermat, adakah rumus dasar yang bisa lansung digunakan untuk menyelesaikan soalnya.
2. kalau tidak ada, periksa dengan cermat persamaannya apakah kita perlu melakukan pemisalan
3. kalau tidak perlu melakukan pemisalan, periksa model matematikanya yang ditanyakan, apakah kita perlu mengubah model itu menjadi model lain.
4. kalau memang harus mengubah modelnya, periksa dengan cermat, apakah kita perlu menggunakan rumus lain sebagai alat bantunya.
5. kalau tidak perlu mengubah modelnya, periksa apakah kita perlu melakukan subtitusi.
6. periksa pula apakah kita perlu melakukan eliminasi.
7. kalau ditanya hubungan antara garis dengan parabolanya, lakukan subtitusi dulu,kemudian periksa diskriminan persamaan kuadratnya.
8. bila diketahui gradient persamaan garisnya, simak dengan cermat, apakah kita membutuhkan rumus-rumus turunan sebagai alat bantunya.
9. periksa dulu apakah kita perlu menggunakan (kiat smar) untuk menyelesaikan pertaksamaan sebagai alat Bantu.
10. kelau soalnya dalam bentuk persamaan tersamar, segera bentuk model matematikanya (model persamaaan kuadratnya), selanjutnya analisis model itu dengan landasan pengetahuan tentang persamaan kuadrat.
Memahami soal yang ada
1. apakah kita mengetahui arti semua kata yang digunakan?, kalau tidak, carilah di indeks, kamus,definisi dana lain sebagainya.
2. apakah kita mengetahui yang dicari atau ditanyakan?
3. apakah kita mampu menyajikan soal dengan menggunakan kata-kata sendiri.
4. apakah soal dapat disajikan dengan cara lain
5. apakah kita dapat menggambar sesuatu yang dapat digunakan sebagai bantuan
6. apakah informasi cukup untuk dapat menyelesaikan soal.
7. apakah informasi berlebihan.
8. apakah ada yang perlu dicari sebelum mencari jawab dari soal.
Menyusun suatu strategi
1. apakah akan membahas berbagai strategi yang ada, tetapi jangan ragu-ragu untuk mencoba salah satu dari strategi untuk digunakan untuk menyelesaikan soal yang kita hadapi.
2. pada umumnya strategi yang berhasil diketemukan seteleh beberapa kali mencoba strategi yang gagal. Kegagalan adalah satu langkah kecil untuk mencapai tujuan yang kita inginkan.
Melakukan strategi yang kita inginkan
Langkah ini lebih mudah disbanding menyusun strategi. Di sisni hanya diperlukan kesabaran dan kehati-hatian untuk menjalankan.
Melihat kembali pekerjaan yagn telah kita lakukan. Selanjutnya, kalau perlu menyusun strategi baru yang lebih baik atau menuliskan jawaban dengan lebih baik.
Karasteristik yang baik bagi orang untuk mampu melakukan problem solving
1. kemampuan mengerti konsep dan istilah matematika.
2. kemampuan untuk mencatat kesamaan, perbedaan dan analogi.
3. kemampuan untuk mengidentifikasi elemen terpenting dan memilih prosedur yang benar.
4. kemampuan untuk mengetahui hal yang tidak berkaitan.
5. kemampuan untuk menaksir dan menganalisa.
6. kemampuan untuk memvisualisasi dana menginterpretasi kuantitas atau ruang.
7. kemampuan untuk memperumum berdasarkan beberapa contoh.
8. kemampuan utnuk berganti metode yang telah diketahui.
9. mempunyai keberanian diri yang cukupdan merasa senang terhadap materinya.
Saran untuk pengajar
1. ajari dengan berbagai strategi yang dapat digunakan untuk berbagai soal
2. berikan waktu yang cukup untuk murid mencoba soal yang ada.
3. ajaklah murid untuk menyelesaikan dengan cara lain.
4. setelah menjawab diperoleh, ajaklah murid untuk melihat kembali, melihat kemungkinan lain, mengatakan dengan bahasa sendir, kemudian ajaklah untuk mencarai penyelesaian dengan cara yang lebih baik.
5. jika kita berhadapan dengan materi yang sulit, tidak berarti kita harus menghindar. Tetapi gunakan cukup waktu untuk mengulang dan mengerjakan soal yang lebih banyak. Mulailah dengan mengerjakan soal serupa, dan kemudian soal-soal yang lebih menantang.
6. fleksibelitas di dalam pemecahan masalah (problem solving) merupakan perilaku belajar yang baik.
Cara lain Menyelesaikan soal pilihan ganda pertidaksamaan
1. Pilihlan sebuah bilangan yang menghasilkan perhitungan yang mudah bila bilangan itu disubtitusikan ke dalam pertaksamaan
2. subtitusikan bilangan yang kita pilih itu ke dalam pertaksamaan dan kemudian periksa kebenaran ketaksamaan yang terjadi.
3. bila ketaksamaan yang terjadi itu benar, himpunan penyelesaian yang benar harus mengandung bilangan yang kita pilih tadi. Namun bila salah, kesimpulannya adalah sebaliknya.
Penyelesaian persamaan kuadrat soal pilihan ganda
• pertama-tama kita ganti dulu peubah yang tidak diketahui nilainya dengan sebuah bilangan nyata sembarang. Bentuk yang terjadi kemudian kita analisis dengan menggunakan rumus-rumus dasar.
1. ajukan pertanyaan yang berkaitan dengan data maupun informasi yang tersedia di dalam soal.
2. Mengambil kesimpulan dengan data atau informasi yang ada dalam soal.
3. Menciptakan cara mudah atau mempercepat untuk menyelesaikan
1. simak dengan cermat, adakah rumus dasar yang bisa lansung digunakan untuk menyelesaikan soalnya.
2. kalau tidak ada, periksa dengan cermat persamaannya apakah kita perlu melakukan pemisalan
3. kalau tidak perlu melakukan pemisalan, periksa model matematikanya yang ditanyakan, apakah kita perlu mengubah model itu menjadi model lain.
4. kalau memang harus mengubah modelnya, periksa dengan cermat, apakah kita perlu menggunakan rumus lain sebagai alat bantunya.
5. kalau tidak perlu mengubah modelnya, periksa apakah kita perlu melakukan subtitusi.
6. periksa pula apakah kita perlu melakukan eliminasi.
7. kalau ditanya hubungan antara garis dengan parabolanya, lakukan subtitusi dulu,kemudian periksa diskriminan persamaan kuadratnya.
8. bila diketahui gradient persamaan garisnya, simak dengan cermat, apakah kita membutuhkan rumus-rumus turunan sebagai alat bantunya.
9. periksa dulu apakah kita perlu menggunakan (kiat smar) untuk menyelesaikan pertaksamaan sebagai alat Bantu.
10. kelau soalnya dalam bentuk persamaan tersamar, segera bentuk model matematikanya (model persamaaan kuadratnya), selanjutnya analisis model itu dengan landasan pengetahuan tentang persamaan kuadrat.
Memahami soal yang ada
1. apakah kita mengetahui arti semua kata yang digunakan?, kalau tidak, carilah di indeks, kamus,definisi dana lain sebagainya.
2. apakah kita mengetahui yang dicari atau ditanyakan?
3. apakah kita mampu menyajikan soal dengan menggunakan kata-kata sendiri.
4. apakah soal dapat disajikan dengan cara lain
5. apakah kita dapat menggambar sesuatu yang dapat digunakan sebagai bantuan
6. apakah informasi cukup untuk dapat menyelesaikan soal.
7. apakah informasi berlebihan.
8. apakah ada yang perlu dicari sebelum mencari jawab dari soal.
Menyusun suatu strategi
1. apakah akan membahas berbagai strategi yang ada, tetapi jangan ragu-ragu untuk mencoba salah satu dari strategi untuk digunakan untuk menyelesaikan soal yang kita hadapi.
2. pada umumnya strategi yang berhasil diketemukan seteleh beberapa kali mencoba strategi yang gagal. Kegagalan adalah satu langkah kecil untuk mencapai tujuan yang kita inginkan.
Melakukan strategi yang kita inginkan
Langkah ini lebih mudah disbanding menyusun strategi. Di sisni hanya diperlukan kesabaran dan kehati-hatian untuk menjalankan.
Melihat kembali pekerjaan yagn telah kita lakukan. Selanjutnya, kalau perlu menyusun strategi baru yang lebih baik atau menuliskan jawaban dengan lebih baik.
Karasteristik yang baik bagi orang untuk mampu melakukan problem solving
1. kemampuan mengerti konsep dan istilah matematika.
2. kemampuan untuk mencatat kesamaan, perbedaan dan analogi.
3. kemampuan untuk mengidentifikasi elemen terpenting dan memilih prosedur yang benar.
4. kemampuan untuk mengetahui hal yang tidak berkaitan.
5. kemampuan untuk menaksir dan menganalisa.
6. kemampuan untuk memvisualisasi dana menginterpretasi kuantitas atau ruang.
7. kemampuan untuk memperumum berdasarkan beberapa contoh.
8. kemampuan utnuk berganti metode yang telah diketahui.
9. mempunyai keberanian diri yang cukupdan merasa senang terhadap materinya.
Saran untuk pengajar
1. ajari dengan berbagai strategi yang dapat digunakan untuk berbagai soal
2. berikan waktu yang cukup untuk murid mencoba soal yang ada.
3. ajaklah murid untuk menyelesaikan dengan cara lain.
4. setelah menjawab diperoleh, ajaklah murid untuk melihat kembali, melihat kemungkinan lain, mengatakan dengan bahasa sendir, kemudian ajaklah untuk mencarai penyelesaian dengan cara yang lebih baik.
5. jika kita berhadapan dengan materi yang sulit, tidak berarti kita harus menghindar. Tetapi gunakan cukup waktu untuk mengulang dan mengerjakan soal yang lebih banyak. Mulailah dengan mengerjakan soal serupa, dan kemudian soal-soal yang lebih menantang.
6. fleksibelitas di dalam pemecahan masalah (problem solving) merupakan perilaku belajar yang baik.
6 Kesalahan Siswa dalam mengerjakan Matematika
Belajar matematika tidak sama dengan belajar pelajaran sejarah, metode menghafal tidak cukup karena matemtika bukanlah ilmu hafalan. Jika anda ingin berhasil mengerjakan soal-soal matematika kuncinya, anda harus banyak berlatih dan memahami rumusnya. Berikut ini adalah kesalahan yang sering dilakukan para siswa dalam mengerjakan soal matematika:
1. Tidak Belajar dan Terlalu Percaya Diri:
Beberapa siswa sering merasa yakin dan sudah puas dengan latihan-latihan yang dilakukan sebelumnya, sehingga pada waktu mendekati ujian mereka tidak belajar sama sekali. Ini merupakan kesalahan yang sangat fatal yang sering dilakukan para siswa. Meskipun anda cerdas dan pandai, sebaiknya persiapkanlah diri anda sebaik mungkin.
2. Belajar Matematika dengan Menghafal dan Tanpa Latihan:
Salah jika anda belajar matematika tanpa latihan, karena sebenarnya banyak yang anda bisa temukan saat latihan. Jangan terlalu banyak membaca konsep karena tidak akan membuat anda mahir dalam mengerjakan soal-soal matematika. Porsi yang tepat adalah 20% untuk membaca konsep dan 80% untuk latihan. Ingat soal matematika bukanlah konsep semata, tetapi lebih banyak soal yang menggunakan rumus, logika, dan menyimpulkan sesuatu,
3. Terburu-buru:
Biasanya kesalahan ini dilakukan karena siswa ingin segera menyelesaikan soal matematika dan mendapatkan nilai yang maksimal. Namun karena terburu-buru banyak kesalahan-kesalahan sepele yang dilakukan. Misalnya ketika mengerjakan soal urain, ada yang salah, kemudian dihapus/di tipex, sambil menunggu kemudian mengerjakan soal yang lain. Karena terburu-buru, maka jawaban yang ingin diperbaiki menjadi kosong dan tidak jadi diperbaiki. Fatal bukan ?
4. Tidak Teliti:
Sayang benar jika anda bisa mengerjakan sebuah soal matematika dengan lengkap, tetapi anda merasa kecewa karena setelah anda keluar dari ruang ujian anda baru menyadari bahwa jawaban Anda salah pada
1. Tidak Belajar dan Terlalu Percaya Diri:
Beberapa siswa sering merasa yakin dan sudah puas dengan latihan-latihan yang dilakukan sebelumnya, sehingga pada waktu mendekati ujian mereka tidak belajar sama sekali. Ini merupakan kesalahan yang sangat fatal yang sering dilakukan para siswa. Meskipun anda cerdas dan pandai, sebaiknya persiapkanlah diri anda sebaik mungkin.
2. Belajar Matematika dengan Menghafal dan Tanpa Latihan:
Salah jika anda belajar matematika tanpa latihan, karena sebenarnya banyak yang anda bisa temukan saat latihan. Jangan terlalu banyak membaca konsep karena tidak akan membuat anda mahir dalam mengerjakan soal-soal matematika. Porsi yang tepat adalah 20% untuk membaca konsep dan 80% untuk latihan. Ingat soal matematika bukanlah konsep semata, tetapi lebih banyak soal yang menggunakan rumus, logika, dan menyimpulkan sesuatu,
3. Terburu-buru:
Biasanya kesalahan ini dilakukan karena siswa ingin segera menyelesaikan soal matematika dan mendapatkan nilai yang maksimal. Namun karena terburu-buru banyak kesalahan-kesalahan sepele yang dilakukan. Misalnya ketika mengerjakan soal urain, ada yang salah, kemudian dihapus/di tipex, sambil menunggu kemudian mengerjakan soal yang lain. Karena terburu-buru, maka jawaban yang ingin diperbaiki menjadi kosong dan tidak jadi diperbaiki. Fatal bukan ?
4. Tidak Teliti:
Sayang benar jika anda bisa mengerjakan sebuah soal matematika dengan lengkap, tetapi anda merasa kecewa karena setelah anda keluar dari ruang ujian anda baru menyadari bahwa jawaban Anda salah pada
baris terakhir saja. Anda sudah mengerjakan dengan susah payah, tetapi karena ketidaktelitian membuat jawaban anda salah. Misalnya: 1+(-10) menjadi 9, padahal hanya kurang tanda (-) saja, betapa itu sangat mengecewakan jika itu terjadi pada anda.
5. Tidak Memperhatikan Petunjuk Soal dan Lupa Menulis Identitas Diri:
Ketika anda mau mengerjakan soal-soal matematika, sebaiknya anda membaca terlebih dahulu petunjuk soalnya. Siapa tahu ada aturan atau petunjuk-petunjuk yang baru atau tidak seperti petunjuk sebelumnya. Misalnya skor setiap nomor, skornya 1 atau 4, jika salah -1 dan lain-lainnya.
6. Mengerjakan Tidak dengan Prioritas dan Tanpa Strategi:
Dalam mengerjakan soal matematika biasanya siswa cenderung mengerjakan dari nomor 1 dan tidak memperhatikan soal-soal yang lain. Akibatnya jika nomor 1 kebetulan soal yang sulit, maka pada bagian awal anda sudah membuat kesalahan. Selain itu anda akan cenderung emosi semisal anda tidak memperoleh jawabannya. Ada tipe pembuat soal yang seperti ini, yang digunakan untuk menguji psikologis siswa. Sebaiknya Anda hati-hati dalam menghadapi tipe-tipe soal yang sulit dan ditaruh di bagian awal soal.
Sebaiknya, anda lihat terlebih dahulu semua soal, jumlah halaman, lengkap atau tidak, prioritaskan soal-soal yang mudah menurut anda, baru kemudian mengerjakan soal-soal yang sulit. Setelah itu Anda hitung kemungkinan anda bisa mengerjakan berapa soal. Sudah tuntas belum ?
Saran kami dalam mengerjakan soal matematika sebaiknya, anda harus:
1. Percaya Diri
2. Mengerjakan dengan Strategi
3. Persiapkan diri dengan Banyak Berlatih
Selamat Belajar Matematika ...
5. Tidak Memperhatikan Petunjuk Soal dan Lupa Menulis Identitas Diri:
Ketika anda mau mengerjakan soal-soal matematika, sebaiknya anda membaca terlebih dahulu petunjuk soalnya. Siapa tahu ada aturan atau petunjuk-petunjuk yang baru atau tidak seperti petunjuk sebelumnya. Misalnya skor setiap nomor, skornya 1 atau 4, jika salah -1 dan lain-lainnya.
6. Mengerjakan Tidak dengan Prioritas dan Tanpa Strategi:
Dalam mengerjakan soal matematika biasanya siswa cenderung mengerjakan dari nomor 1 dan tidak memperhatikan soal-soal yang lain. Akibatnya jika nomor 1 kebetulan soal yang sulit, maka pada bagian awal anda sudah membuat kesalahan. Selain itu anda akan cenderung emosi semisal anda tidak memperoleh jawabannya. Ada tipe pembuat soal yang seperti ini, yang digunakan untuk menguji psikologis siswa. Sebaiknya Anda hati-hati dalam menghadapi tipe-tipe soal yang sulit dan ditaruh di bagian awal soal.
Sebaiknya, anda lihat terlebih dahulu semua soal, jumlah halaman, lengkap atau tidak, prioritaskan soal-soal yang mudah menurut anda, baru kemudian mengerjakan soal-soal yang sulit. Setelah itu Anda hitung kemungkinan anda bisa mengerjakan berapa soal. Sudah tuntas belum ?
Saran kami dalam mengerjakan soal matematika sebaiknya, anda harus:
1. Percaya Diri
2. Mengerjakan dengan Strategi
3. Persiapkan diri dengan Banyak Berlatih
Selamat Belajar Matematika ...
Belajar Integral
Matematic terus menantang saya agar berinovasi menemukan cara belajar kalkulus yang mudah dan asyik. Tahap demi tahap saya mulai menemukan inovasi yang diharapkan
Pemahaman tentang luas bidang menjadi dasar utama integral. Penggunaan istilah yang tepat akan sangat membantu kita.
Luas segi empat adalah panjang x lebar = p x l.
Dalam koordinat cartesius yang mengacu titik asal O(0,0) maka luas segi empat adalah p x l = a.t = x.y.
Luas segitiga adalah 1/2 panjang x lebar = 1/2 p x l = 1/2 a.t = 1/2 x.y
Luas bidang di bawah kurva y = x^2 adalah
1/3 a.t = 1/3 x.y = 1/3 x.x^2 = 1/3 x^3
(Sesuai dengan hasil integral x^2)
Luas bidang di bawah kurva y = x^3 adalah
1/4 a.t = 1/4 x.y = 1/4 x.x^3 = 1/4 x^4
Sesuai dengan hasil integral x^3.
Kata-kata diatas nampak sederhana. Tetapi tidak selalu mudah untuk diterapkan. Bila berhasil menerapkannya memang menjadi sederhana dan mudah.
Dalam belajar integral kalkulus misalnya, saya terus berusaha menemukan formula-formula yang sederhana. Dengan mengujikan formula dan notasi kepada anak-anak, saya memperoleh banyak feedback.
Pemilihan notasi integral, misalnya, sangat berpengaruh besar. misalnya pada:
Notasi Leibniz adalah notasi paling mantab menurut saya pribadi dan para guru matematika. Tetapi bagi anak-anak, notasi Leibniz tidak mudah dipahami.
Notasi huruf s yang dipanjangkan (seperti cacing), dx, batas atas, batas bawah, dan C cukup memecah konsentrasi anak-anak untuk menangkap pesan utama dari integral itu sendiri.
Notasi Newton untuk integral memang tidak banyak yang menggunakan. Newton memberi tanda garis vertikal di atas fungsi. Notasi ini ambigu dengan banyak notasi lain. Saya juga tidak merekomendasikan notasi ini untuk para siswa-siswi.
Notasi Euler untuk diferensial adalah Dx. Sedangkan untuk integral dapat kita pandang sebagai antidiferensial dengan notasi Ax. Saya pikir notasi Euler cukup sederhana. Tetapi bagi anak-anak, masih belum cukup sederhana.
Tentu masih banyak alternatif notasi-notasi lain. Lalu muncul ide, “Mengapa tidak membuat notasi sendiri saja?”
Dengan tujuan utama memudahkan proses pembelajaran integral kalkulus di penjelasan yang saya contohkan ini menggunakan notasi tanda panah saja.
misalnya:
Dengan notasi sederhana seperti di atas, anak-anak sangat terbantu. Mereka dapat langsung fokus pada kata-kata utamanya yaitu integral itu sendiri. Mereka tidak merasa diperumit dengan notasi-notasi yang tidak akrab.
Integral 2sinxdx + Integral (5-2x)dx. Agar lebih mudah selesaikan satu persatu.
Integral 2sinxdx = -2cosx + C
Integral Cos (5-2x)dx pakai lagi substitusi.
5-2x = U
-2dx = dU
dx= -1/2 du
Nah ganti lagi seperti yang tadi:
Integral Cos U. -1/2 du.
Ingat -1/2 bisa dipindah ke depan. Jadinya:
-1/2 Integral Cos U du = -1/2 Sin U + C
Kembalikan lagi yang tadi diganti.
= -1/2 Sin (5-2x) +C
Gabungan keduanya.
Jadi hasil akhirnya adalah -2 cos x - 1/2 Sin (5-2x) +C
Perhatian: C-nya cukup ditulis sekali lagi atau digabungin jadi satu. Karena c adalah konstanta.
Apabila telah memahami silakan kerjakan soal berikut ini:
Integral 2xSin(x^2+5)dx
Selamat berlatih.
Pemahaman tentang luas bidang menjadi dasar utama integral. Penggunaan istilah yang tepat akan sangat membantu kita.
Luas segi empat adalah panjang x lebar = p x l.
Dalam koordinat cartesius yang mengacu titik asal O(0,0) maka luas segi empat adalah p x l = a.t = x.y.
Luas segitiga adalah 1/2 panjang x lebar = 1/2 p x l = 1/2 a.t = 1/2 x.y
Luas bidang di bawah kurva y = x^2 adalah
1/3 a.t = 1/3 x.y = 1/3 x.x^2 = 1/3 x^3
(Sesuai dengan hasil integral x^2)
Luas bidang di bawah kurva y = x^3 adalah
1/4 a.t = 1/4 x.y = 1/4 x.x^3 = 1/4 x^4
Sesuai dengan hasil integral x^3.
Kata-kata diatas nampak sederhana. Tetapi tidak selalu mudah untuk diterapkan. Bila berhasil menerapkannya memang menjadi sederhana dan mudah.
Dalam belajar integral kalkulus misalnya, saya terus berusaha menemukan formula-formula yang sederhana. Dengan mengujikan formula dan notasi kepada anak-anak, saya memperoleh banyak feedback.
Pemilihan notasi integral, misalnya, sangat berpengaruh besar. misalnya pada:
Notasi Leibniz adalah notasi paling mantab menurut saya pribadi dan para guru matematika. Tetapi bagi anak-anak, notasi Leibniz tidak mudah dipahami.
Notasi huruf s yang dipanjangkan (seperti cacing), dx, batas atas, batas bawah, dan C cukup memecah konsentrasi anak-anak untuk menangkap pesan utama dari integral itu sendiri.
Notasi Newton untuk integral memang tidak banyak yang menggunakan. Newton memberi tanda garis vertikal di atas fungsi. Notasi ini ambigu dengan banyak notasi lain. Saya juga tidak merekomendasikan notasi ini untuk para siswa-siswi.
Notasi Euler untuk diferensial adalah Dx. Sedangkan untuk integral dapat kita pandang sebagai antidiferensial dengan notasi Ax. Saya pikir notasi Euler cukup sederhana. Tetapi bagi anak-anak, masih belum cukup sederhana.
Tentu masih banyak alternatif notasi-notasi lain. Lalu muncul ide, “Mengapa tidak membuat notasi sendiri saja?”
Dengan tujuan utama memudahkan proses pembelajaran integral kalkulus di penjelasan yang saya contohkan ini menggunakan notasi tanda panah saja.
misalnya:
Code:
x → 1/2 x^2 Kita membacanya: Integral x adalah 1/2 x^2 2x → x^2 Integral 2x adalah x^2
Pada kesempatan kali ini, kita akan coba memecahkan integral trigonometri.
Untuk memecahkan integral trigonometri dapat dipergunakan metoda subsitusi atau penggantian. Yakni berusaha dijadikan sin u du atau cos u du. Selanjutnya gunakan rumus-rumus dasar, seperti Integral Sin x = -Cos x + C dan Integral Cos x = sin x. Mari perhatikan soal-soal berikut ini.
soal 1. Integral sin (5x+10)dx
misalkan 5x+10= u
diturunkan atau dideferensial
khan jadi: 5dx=du.
dx= 1/5 du.
masukkan lagi ke rumus di atas.
5x+10 diganti ama u dan dx diganti ma 1/5 du jadinya:
Integral sin u. 1/5 du.
1/5 boleh dipindah ke depan.
1/5 (Integral (sin u du))= 1/5 (-Cos u) + C
=-1/5 Cos u+C
Kembalikan lagi u-nya dengan 5x+10; jadinya adalah:
-1/5 Cos (5x+10) + C
soal kedua:
Integral (2sinx + cos(5-2x))dx jadi
misalkan 5x+10= u
diturunkan atau dideferensial
khan jadi: 5dx=du.
dx= 1/5 du.
masukkan lagi ke rumus di atas.
5x+10 diganti ama u dan dx diganti ma 1/5 du jadinya:
Integral sin u. 1/5 du.
1/5 boleh dipindah ke depan.
1/5 (Integral (sin u du))= 1/5 (-Cos u) + C
=-1/5 Cos u+C
Kembalikan lagi u-nya dengan 5x+10; jadinya adalah:
-1/5 Cos (5x+10) + C
soal kedua:
Integral (2sinx + cos(5-2x))dx jadi
Integral 2sinxdx + Integral (5-2x)dx. Agar lebih mudah selesaikan satu persatu.
Integral 2sinxdx = -2cosx + C
Integral Cos (5-2x)dx pakai lagi substitusi.
5-2x = U
-2dx = dU
dx= -1/2 du
Nah ganti lagi seperti yang tadi:
Integral Cos U. -1/2 du.
Ingat -1/2 bisa dipindah ke depan. Jadinya:
-1/2 Integral Cos U du = -1/2 Sin U + C
Kembalikan lagi yang tadi diganti.
= -1/2 Sin (5-2x) +C
Gabungan keduanya.
Jadi hasil akhirnya adalah -2 cos x - 1/2 Sin (5-2x) +C
Perhatian: C-nya cukup ditulis sekali lagi atau digabungin jadi satu. Karena c adalah konstanta.
Apabila telah memahami silakan kerjakan soal berikut ini:
Integral 2xSin(x^2+5)dx
Selamat berlatih.
Tips Matematika
Ada tips ringan yang bisa menarik minat anak-anak, terutama yang sudah bisa melakukan perhitungan (tambah, kurang, bagi, kali). Tips ini sering saya gunakan dan selalu sukses menarik minat. Karena sifatnya yang universal, orang dewasapun bisa menggunakannya dalam kegiatan sehari-hari. Ada yang bilang hanya tips menghitung cepat, namun saya melihatnya ada hal yang lebih fundamental. Mari kita simak tips ini.
1. Pembagian dan Perkalian 2
Jika anda ditanya, berapa 4 X 10, 2 X 10, 1200 X 10 dan lain sebagainya perkalian dengan 10, 100, 1000, pasti dengan cepat dan mudah kita menemukan jawabannya. Mengapa mudah, karena kita hanya perlu menambahkan angka nol dibelakang angka yang dikalikan dengan angka bermodel kelipatan 10.
Bagaimana dengan perkalian angka 5 ? Hampir mirip. Perkalian angka 5 sama saja dengan mengalikannya dengan angka 10 dan membaginya dengan angka 2. (5 = 10/2, isn’t it ? :-D )
Pengalaman saya, perhitungan angka genap lebih mudah diolah diotak saya dibandingkan angka ganjil. Jika diminta jawaban 75 X 5, saya akan menghitungnya sebagai 75 X (10 : 2), alias 750 : 2 = 375.
Coba test anak-anak untuk menghitung perhitungan angka (perkalian dan pembagian) dengan angka ganjil dan membandingkannya dengan perhitungan angka genap. Saya yakin sebagian besar lebih cepat menghitung perhitungan angka genap.
Keistimewaan angka 2 ini bisa dikembangkan untuk menjawab secara cepat perhitungan yang tidak bisa dicerna secara langsung.
Contoh, berapa hasil perkalian 12,5 X 8 atau 6,25 X 8 ? Alih-alih mengalikannya secara langsung, saya akan lebih cepat menghitungnya dengan merubah angka ganjil menjadi genap dengan mengalikannya dengan angka 2 dan membagi rekannya yang genap dengan angka 2.
12,5 X 8 ==> 25 X 4 ==> 50 X 2 ==> 100. Posisi perhitungan bisa dibatasi pada model persamaan yang sudah bisa langsung dicerna, dalam contoh diatas bisa dibatasi pada 25 X 4.
6,25 X 8 ==> 12,5 X 4 ==> 25 X 2 ==> 50
Model hitung cepat diatas mungkin menggunakan sample yang mudah-mudah saja (kalau masih menggunakan sample yang sulit ya anak-anak tambah males belajar matematika dunk :-) ) tapi bisa dilihat bahwa model perhitungan tersebut bisa dimanfaatkan untuk bilangan yang lainnya, dengan syarat salah satu pengali adalah genap.
Kalau ditanya 12,5 X 6,25 ya model diatas tidak berlaku…
Jika perlu, kita bisa melakukan kombinasi perkalian 5, 2 maupun 10 sekaligus, tergantung situasi dan contoh soal yang diberikan.
Misalnya, 4,75 X 400 ==> 475 X 4 ==> 950 X 2 ==> 1900
2. Selisih Dua Kuadrat & Dua Pengkuadratan yang Penting
Saya mendapatkan materi ini di SMP (SMPN I Tambun Selatan Bekasi). Dulu saya tidak begitu memahaminya dan menganggap ini materi pelajaran yang dihapal, namun ternyata ada hal yang penting dan bisa dijadikan tips untuk menarik minat para bocah :-) .
Dengan pengetahuan pada tips 1, coba lontarkan pertanyaan berikut :
Berapa hasil perkalian 12 X 8 ?
Berapa hasil perkalian 29 X 31 ?
Berapa hasil perkalian 25 X 15 ?
Untuk pertanyaan pertama, tips 1 masih bisa digunakan namun untuk yang kedua dan ketiga, tips kesatu sulit digunakan karena keduanya sama-sama ganjil. Meski demikian kita bisa tetap menghitungnya secara cepat karena kedua bilangan yang digunakan istimewa.
12 X 8 = 96 –> jangan pakai kalkulator ya, dan mikirnya jangan lama-lama, malu sama anak SD.
29 X 31 = 899
25 X 15 = 375
29 X 31 bisa dijadikan persamaan (30-1) X (30+1) ==> 302-12 ==> 900-1 ==> 899
25 X 15 bisa dijadikan persamaan (20+5) X (20-5) ==> 202-52 ==> 400-25 ==> 375
Tips kedua ini bisa dipakai dengan syarat kedua perkalian bisa dipecah menjadi model yang sama sehingga nantinya berlaku rumus :
(A+B) X (A-B) = A2 – B2
Dua tips diatas semestinya bisa kita manfaatkan untuk menunjukkan bahwa matematika itu menyenangkan untuk dipelajari dan dapat diaplikasikan langsung dikehidupan sehari-hari.
Banyak yang bilang, orang sukses tidak hanya ditentukan oleh kemampuan matematika. Bnayak orang sukses meski matematikanya jeblok karena bisa mengembangkan kemampuan sosial dan humaniora. Menurut saya, diskursus masalah ini sebaiknya diposisikan untuk memacu prestasi anak yang kurang memiliki kemampuan dibidang ilmu eksakta, bukan sebagai generalisasi bahwa matematika tidak penting.
1. Pembagian dan Perkalian 2
Jika anda ditanya, berapa 4 X 10, 2 X 10, 1200 X 10 dan lain sebagainya perkalian dengan 10, 100, 1000, pasti dengan cepat dan mudah kita menemukan jawabannya. Mengapa mudah, karena kita hanya perlu menambahkan angka nol dibelakang angka yang dikalikan dengan angka bermodel kelipatan 10.
Bagaimana dengan perkalian angka 5 ? Hampir mirip. Perkalian angka 5 sama saja dengan mengalikannya dengan angka 10 dan membaginya dengan angka 2. (5 = 10/2, isn’t it ? :-D )
Pengalaman saya, perhitungan angka genap lebih mudah diolah diotak saya dibandingkan angka ganjil. Jika diminta jawaban 75 X 5, saya akan menghitungnya sebagai 75 X (10 : 2), alias 750 : 2 = 375.
Coba test anak-anak untuk menghitung perhitungan angka (perkalian dan pembagian) dengan angka ganjil dan membandingkannya dengan perhitungan angka genap. Saya yakin sebagian besar lebih cepat menghitung perhitungan angka genap.
Keistimewaan angka 2 ini bisa dikembangkan untuk menjawab secara cepat perhitungan yang tidak bisa dicerna secara langsung.
Contoh, berapa hasil perkalian 12,5 X 8 atau 6,25 X 8 ? Alih-alih mengalikannya secara langsung, saya akan lebih cepat menghitungnya dengan merubah angka ganjil menjadi genap dengan mengalikannya dengan angka 2 dan membagi rekannya yang genap dengan angka 2.
12,5 X 8 ==> 25 X 4 ==> 50 X 2 ==> 100. Posisi perhitungan bisa dibatasi pada model persamaan yang sudah bisa langsung dicerna, dalam contoh diatas bisa dibatasi pada 25 X 4.
6,25 X 8 ==> 12,5 X 4 ==> 25 X 2 ==> 50
Model hitung cepat diatas mungkin menggunakan sample yang mudah-mudah saja (kalau masih menggunakan sample yang sulit ya anak-anak tambah males belajar matematika dunk :-) ) tapi bisa dilihat bahwa model perhitungan tersebut bisa dimanfaatkan untuk bilangan yang lainnya, dengan syarat salah satu pengali adalah genap.
Kalau ditanya 12,5 X 6,25 ya model diatas tidak berlaku…
Jika perlu, kita bisa melakukan kombinasi perkalian 5, 2 maupun 10 sekaligus, tergantung situasi dan contoh soal yang diberikan.
Misalnya, 4,75 X 400 ==> 475 X 4 ==> 950 X 2 ==> 1900
2. Selisih Dua Kuadrat & Dua Pengkuadratan yang Penting
Saya mendapatkan materi ini di SMP (SMPN I Tambun Selatan Bekasi). Dulu saya tidak begitu memahaminya dan menganggap ini materi pelajaran yang dihapal, namun ternyata ada hal yang penting dan bisa dijadikan tips untuk menarik minat para bocah :-) .
Dengan pengetahuan pada tips 1, coba lontarkan pertanyaan berikut :
Berapa hasil perkalian 12 X 8 ?
Berapa hasil perkalian 29 X 31 ?
Berapa hasil perkalian 25 X 15 ?
Untuk pertanyaan pertama, tips 1 masih bisa digunakan namun untuk yang kedua dan ketiga, tips kesatu sulit digunakan karena keduanya sama-sama ganjil. Meski demikian kita bisa tetap menghitungnya secara cepat karena kedua bilangan yang digunakan istimewa.
12 X 8 = 96 –> jangan pakai kalkulator ya, dan mikirnya jangan lama-lama, malu sama anak SD.
29 X 31 = 899
25 X 15 = 375
29 X 31 bisa dijadikan persamaan (30-1) X (30+1) ==> 302-12 ==> 900-1 ==> 899
25 X 15 bisa dijadikan persamaan (20+5) X (20-5) ==> 202-52 ==> 400-25 ==> 375
Tips kedua ini bisa dipakai dengan syarat kedua perkalian bisa dipecah menjadi model yang sama sehingga nantinya berlaku rumus :
(A+B) X (A-B) = A2 – B2
Dua tips diatas semestinya bisa kita manfaatkan untuk menunjukkan bahwa matematika itu menyenangkan untuk dipelajari dan dapat diaplikasikan langsung dikehidupan sehari-hari.
Banyak yang bilang, orang sukses tidak hanya ditentukan oleh kemampuan matematika. Bnayak orang sukses meski matematikanya jeblok karena bisa mengembangkan kemampuan sosial dan humaniora. Menurut saya, diskursus masalah ini sebaiknya diposisikan untuk memacu prestasi anak yang kurang memiliki kemampuan dibidang ilmu eksakta, bukan sebagai generalisasi bahwa matematika tidak penting.








